Защо откриването на структури и модели е важно и как да развиваме това умение с помощта на математически рутини?
Когато учениците получат задача в час по математика, те имат нагласата, че трябва бързо да намерят решението и често се притесняват дали ще открият верния отговор. Независимо дали са водени от състезателни мотиви за доказване на интелектуалните си компетентности, или от страха, че няма да се справят със задачата, напрежението пречи на тяхното пълноценно ангажиране в учебния процес.
За да могат децата да осмислят, разсъждават, да формулират аргументи, критика или да изграждат модел, те първо трябва да могат да забелязват – да виждат подробности (както очевидни, така и по-трудно забележими), докато разглеждат даден проблем. Някои ученици веднага забелязват важната информация в математическите задачи и правят обосновани предложения за решаването им. За съжаление, не всички ученици се справят така безпроблемно. Затова е важно да изградим у тях необходимите умения, благодарение на които ще бъдат наблюдателни и постоянни при решаване на даден проблем. Мисловните рутини за развиване на наблюдателност са стратегия за обучение, с която можем да помогнем на всички ученици да развиват математическото си мислене и да подобряват способността си да осмислят проблемите.
Защо откриването на структури и модели е важно за развиването на математическото мислене на учениците?
Рутините за откриване на структури и модели помагат на учениците да се абстрахират от конкретната задача и да се потопят в предварително зададения контекст. За разлика от стандартните задачи по математика, за чието решаване има определен алгоритъм, при тези рутини учениците могат да открият различни възможни пътища за достигане до крайния резултат.
Изследването на математическите казуси помага на учениците да:
- направят връзка между разсъжденията си и изучаваните принципи и закономерности;
- откриват детайли в дадения проблем;
- забавят темпото и да осмислят задачата, преди да започнат да пресмятат;
- отбележат информация, която може да им бъде полезна по-късно;
- определят аспекти на задачата, които са неясни или объркващи;
- помислят за възможни пътища за решаване на казуса;
- измислят много и различни стратегии;
- генерират въпроси, свързани с казуса, на които им е интересно да открият отговорите.
Как да тренираме наблюдателността на учениците?
Развиването на наблюдателността изисква практика и търпение, време за самостоятелно обмисляне и отбелязване. Същевременно разглеждането на математическите проблеми от различна гледна точка и откриването на нови структури и модели изисква обсъждане на генерираните идеи с другите. Всичко забелязано е важно, дори да не е свързано с изучавания материал. Затова трябва да планираме време за индивидуална работа, за работа в малки групи и за обсъждане с целия клас.
Ето един пример за провеждане на рутина за забелязване на структури и модели:
- Раздайте на всеки ученик по един работен лист или обикновен лист за водене на записки. Помолете учениците да запишат всичко, което са забелязали в предложената задача. Обяснете им, че на този етап не трябва да пресмятат нищо, а само да наблюдават и да записват забелязаните структури, модели и закономерности. Учениците работят самостоятелно и записват идеите си в рамките на 1-2 минути.
- Разделете учениците в групи по двама. Всеки от тях трябва да сподели идеите си с другия, след което всеки трябва да запише в работния си лист тези идеи на партньора си, които самият той не е забелязал. Наблюдавайте процеса и откритията, които учениците са направили. Това ще ви помогне да насочвате дискусията с класа в желаната от вас посока.
- “Дирижирайте” дискусия с целия клас, като посочвате определени ученици да споделят наблюденията си. Започнете от очевидните (цвят, форма) и постепенно надградете с по-сложни наблюдения. Учениците трябва да записват всички наблюдения, които те самите не са установили в етапа на самостоятелна работа.
- В идеалния случай ще имате възможност да посочите ученици, чиито открития са свързани в известна степен с учебния материал. Но дори избраният тип казус да не е свързан директно с него, учениците пак ще имат полза от изследването, споделянето, сравняването и критикуването на своето и чуждото мислене. Всичко това развива способностите им да търсят модели и структури, да забелязват детайли и да разглеждат проблемите от различни гледни точки.
Безплатен бюлетин с ресурси
Запиши се, за да получаваш всяка седмица практични ресурси и идеи

Какви рутинни задачи са подходящи за развиването на наблюдателност?
На практика всяко графично изображение е подходящо за провеждането на този тип рутини. Ето няколко примера за рутини за наблюдателност, които можете да използвате във вашите часове по математика:
-
Картинни уравнения
При този тип задачи различни комбинации от изображения се равняват на различни числа. С помощта на вече решените уравнения учениците трябва да намерят отговора на последното уравнение. За начало учениците трябва да запишат всичко, което са забелязали, без да правят пресмятания.
Някои примерни наблюдения могат да бъдат:
- има три различни вида предмети;
- на повечето места предметите са по един;
- на едно място всеки от предметите е двоен;
- на всеки от редовете присъстват всички предмети;
- в уравненията са използвани операциите събиране, изваждане и умножение;
- в първите две уравнения има повтаряща се структура (обувка + топка).
Могат ли тези наблюдения да помогнат за намирането на правилния отговор?
Решаването на задачата може да бъде следващата стъпка, но самата рутина не е фокусирана върху търсенето на решение. Целта е създаването на навици за изследване и наблюдаване, които са необходими на учениците, за да могат да осмислят различни математически казуси.
-
Кое е излишното?
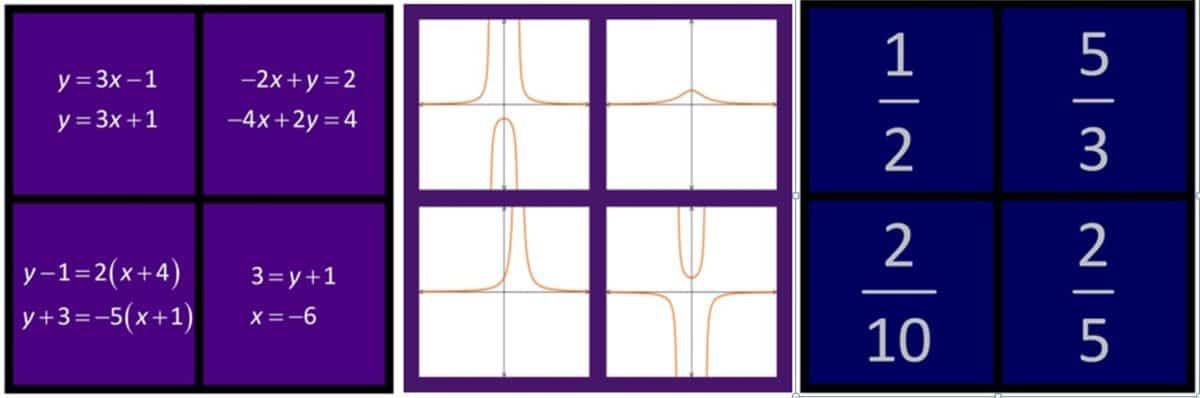
Тази рутина има за цел откриване на сходни и различни характеристики между различни обекти. На учениците се предоставят четири сходни изображения и те трябва да определят кое от тях е излишно. Такъв тип задачи често се предлагат на деца от предучилищна възраст за разграничаване на основни характеристики. Макар да изглеждат елементарни, те всъщност могат да бъдат адаптирани към различно съдържание и да имат различни степени на трудност, което ги прави приложими във всички образователни степени.
Ето няколко примера, които са подходящи за 5. – 7. клас:
Източник: WODB
Тази рутина предлага възможности за множество различни решения, дискусии и търсене на аргументи. В зависимост от признака, по който се сравняват, на практика всяко едно от изображенията може да бъде излишното. Няма верен или грешен отговор. Фокусът е върху развиването на наблюдателността на учениците и вземането на аргументирано решение.
Например, ако разгледаме задачата с обикновените дроби, учениците могат да направят някои от следните наблюдения:
- всички числа са обикновени дроби;
- само една от дробите може да бъде съкратена;
- има само една неправилна дроб, която може да бъде представена като смесено число;
- само едно от числата е по-голямо от 1;
- след съкращаване, само една от дробите има четен знаменател.
За провеждане на дейността можете да използвате този работен лист, а в сайта на английски език можете да намерите още примери за такъв тип задачи.
В следващ етап можете да надградите дейността, като разделите учениците в няколко екипа и ги окуражите да измислят подобен тип задачи, в които да има няколко възможни отговора. След това екипите трябва да разменят задачите помежду си. Всяка група трябва да предложи поне 2 решения на задачата на другия екип. Запишете предложенията на дъската. Съвпада ли броят на решенията с предварително замисления? Има ли варианти, които групата, създала задачата, не е предвидила?
Изтеглете и примерен работен лист за създаване на дизайн на задачата.
-
Пресметни напряко
Тази рутина предлага на учениците техника за откриване на структури и използването им с цел по-лесно пресмятане.
Обяснете на учениците, че ще им покажете изображение, което ще могат да наблюдават в рамките само на 2 секунди. За това време те трябва да отбележат всичко, което им е направило впечатление, както и да генерират идеи за “преки пътища за решаване на задачата”. Всеки ученик записва идеите си, след което ги споделя с ученика до себе си. Следва обсъждане с целия клас. Посочете ученици, които да споделят наблюденията си и ги запишете на дъската.
Разделете учениците в 3-4 групи, след което им покажете изображението отново. Този път им дайте на разположение 3-5 минути да наблюдават и дискутират по групи как могат лесно да пресметнат задачата. Всички групи трябва да предложат вариант за решаване на задачата, като обяснят кои от записаните на дъската наблюдения са използвали.
Ето един пример: учениците трябва да открият лесен начин за пресмятане на броя на фигурите, които изграждат следното изображение:
Тази математическа рутина развива способността на учениците да откриват структури и модели, които след това да използват за по-лесното решаване на различните казуси. Откритите структури се основават на вече изучените математически принципи и понятия. По този начин учениците затвърждават усвоените знания и намират ситуации, в които да ги използват.
Рутините за наблюдателност дават възможност на учениците да осмислят по-добре математическите казуси, да откриват структури и модели, които да използват за по-лесното им решаване. Освен това помагат за затвърждаването на вече усвоения учебен материал и употребата на математически език. Използването на мисловни рутини в часовете по математика създава приятна и безопасна за учениците среда за учене и по този начин променя нагласите и очакванията към дисциплината.
А вие как развивате наблюдателността на учениците си?
Споделете опита си с нас и участвайте в “Добрите практики на фокус”.
За статията са използвани следните ресурси, които са допълнени с личния опит на автора: