“Разочароващи, но не и учудващи” - така просветният министър описа резултатите на българските ученици от международното изследване PISA за 2018 година. Малко по-добри от тези по четене, но все още значително под средното равнище за ОИСР са резултатите ни по математика и по природни науки, въпреки че наши представители ежегодно се завръщат с медали от олимпиади именно в тези области.
Как всъщност PISA оценява учениците в областта на математиката и природните науки?
Математиката е сред областите, в които представянето на учениците се оценява от PISA. За целите на програмата математическата грамотност е дефинирана1 като способността да се формулира, използва и тълкува математическо познание в многообразие от ситуации. Това включва много повече от възпроизвеждането на математическите концепции и процедури, изучавани в училище. PISA се стреми да измери колко добре учениците могат да прилагат в различни области и ситуации знанията си по математика - математическо мислене, математически понятия, процедури, факти, средства и методи за описване, обясняване и прогнозиране на многообразие от явления в реален контекст.
Как се оценява математическата грамотност в PISA 2018
PISA 2018 включва математически задачи, описващи конкретен контекст и произтичащия от него проблем. Учениците трябва да решат проблема посредством познатите им средства на математиката или като използват знания от междупредметни връзки.
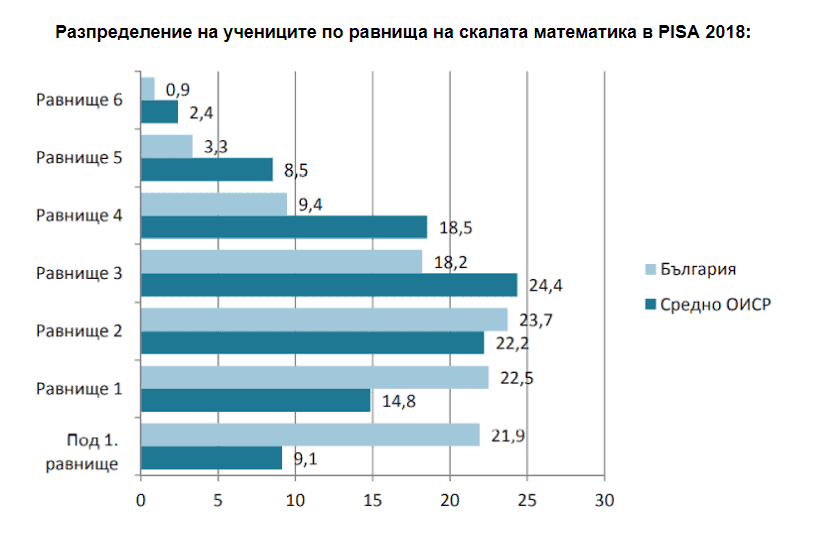
Подобно на тази за четивната грамотност, скàлата за математика2 , е разделена на шест равнища на постижения, като най-ниско е първото, а най-високо - шестото. Нивата са структурирани в йерархичен порядък - т.е. ученик, отговорил правилно на въпросите от по-горно равнище, би следвало да може да реши и въпросите от по-ниските равнища на скàлата. Средният резултат на даден ученик показва на кое равнище съответстват най-трудните задачи, които той може да реши. Всяко равнище на постижения по математика включва около 70 точки, а за базово и тук, както при четенето, е определено второ равнище. Ученици, които не могат да достигнат резултат от второ равнище, се считат за функционално неграмотни по математика. Те се затрудняват да правят преки изводи, да прилагат основни алгоритми, формули, процедури. Не демонстрират математическо мислене и не могат да използват знанията си в сравнително нестандартен контекст.
Както и при четенето, така и по математика “отличници” в PISA 2018 са Китай (591 точки), Сингапур (569 точки), Макао, Китай (558 точки), Хонконг, Китай (551 точки), Китайски Тайпе (523 точки).
Какво показват данните за България
Средният резултат на България е 436 точки, което е статистически значимо по-ниско от средното за ОИСР от 500 точки. Представянето на учениците ни нито се е подобрило, нито се е влошило в сравнение с изданието на PISA през 2015 година (тогава 441 точки).
Тревожен е делът на българските ученици, които не достигат базовото второ равнище. 44,4 % от 15-годишни ученици у нас (при средно 23,9 % за ОИСР) са функционално неграмотни по математика. Учениците с резултати на пето и шесто равнище са малко, но обнадеждаващото е, че делът им е по-висок от този по четене. 4,2 % (при средно за ОИСР 9,4 %) са достигнали най-високите равнища от скалата по математика в PISA 2018.
У нас момичетата се справят средно с 2 точки по-добре от момчетата, макар разликата да не е статистически значима. Обратното, в ОИСР момчетата имат със средно 5 точки по-добър резултат.
Откакто България участва в оценяването, се наблюдава леко подобрение на резултатите, основно в годините между 2006 и 2012. Реално постиженията на учениците ни поддържат едно константно, но ниско равнище.
Какво представлява природонаучната грамотност в PISA
Природните науки са една от ключовите области, включени за оценяване в PISA, като през изданията за 2006 и 2015 година заемат централно място. Под природонаучна грамотност в PISA се разбира способността на учениците да използват познания и информация, да разбират как научното познание променя начина, по който индивидът си взаимодейства с природата, и как това взаимодействие може да бъде използвано за постигане на конкретни цели3.
Чрез новия начин за провеждане на изследването - на компютър - в PISA 2015 за първи път се използват компютърни симулации на експерименти, което дава възможност да се оценят способностите на учениците до провеждат научни изследвания и да интерпретират получените данни и доказателства.
Как се оценява компетентността в областта на природните науки
Подобно на оценяването на четивната грамотност и математиката, в областта на природните науки се използва скала4 . Всяко равнище на скалата описва знанията и уменията, които са необходими за решаването на съответните задачи. Най-ниско е първото (съответно първо А и B) ниво, а най-високо – шестото. За базово и тук се приема второто равнище. Структурата на скалата е йерархична, което означава, че ученик, успешно отговорил на въпросите от по-горното равнище, вероятно би могъл да реши и въпросите от по-ниските равнища на скалата.
Прави впечатление, че в държавите/регионите с най-висок среден резултат по природни науки в PISA 2018 е най-голям и процентът ученици, достигнали второ или по-високо равнище - съответно 97,9 % в Китай, 94,0 % в Макао, Китай, 91, 2% в Естония и 91,0 % в Сингапур.
Как се представят българските ученици
Учениците от България са постигнали среден резултат от 424 точки, което е под средните 500 точки за ОИСР. Но по-тревожно е, че докато 78% от учениците в ОИСР са природонаучно грамотни, за България този дял е едва 53,5 %. Преобладаващо нашите представители са се справили със задачи от 3. и по-ниско ниво:
Много малко на брой са българските ученици, достигнали пето и шесто равнище - едва 1,5 %. Сред резултатите на българските ученици преобладават първо и второ равнище.
В сравнение с предходното издание на PISA, през 2018 година наблюдаваме спад в постиженията на българските ученици от 22 точки. Това вероятно е резултат от по-големия брой грешни отговори на няколко конкретни задачи, защото цялостно в изследването не се забелязва научна област, в която българските младежи да се справят по-лошо от предишни издания на PISA. Няма и големи промени нито в учебните програми, нито в броя или организацията на часовете по природни науки в училище. Като цяло, представянето на нашите ученици от 2006 година насам е константно, но слабо спрямо средния резултат от 500 точки за ОИСР.
В заключение може да се каже, че младежите, които се справят със задачи от най-високо ниво в областта на математиката и в областта на природните науки (и част от които всъщност носят медалите от международни олимпиади и състезания) представляват един наистина малък дял от учениците у нас. Преобладаващо нашите ученици имат по-скоро теоретична подготовка и изпитват затруднения, когато трябва да приложат знанията си в практически ситуации.
Но добрата новина е, че изследвания като PISA ни дават добър ориентир за това къде са слабите ни места и върху какво трябва да поработим. Битката е във всяка класна стая ежедневно, а резултатите, надяваме се, ще видим съвсем скоро!
Всички визуализации в статията са взети от националната извадка за България, с която може да се запознаете в детайли ето тук. Пълните резултати от PISA 2018 са публикувани за областите четене, математика и природни науки ето тук.
__________________________________
1 PISA 2018 заимства дефиницията за математическа грамотност от използваната през 2012 г., когато математиката беше основна област на оценяване. Конкретно, тук се включват уменията на учениците:
- да разпознават проблемите от реалността, които могат да бъдат решени със средствата на математиката;
- да ги решат, като използват математически знания и методи;
- да тълкуват получените резултати от гледна точка на поставения проблем;
- да представят резултатите си.
2
Таблица 1. Скала за оценяване на постиженията на учениците по математика в PISA 2018:
| Равнище | Точки | Характеристика на равнището и задачите, оценяващи способностите на учениците |
| 6 | 669 | Учениците с резултати на шесто равнище успешно решават най-трудните задачи от теста на PISA по математика. Те разбират и използват понятия, обобщават и прилагат информация, като се основават на самостоятелно изследване и моделиране на сложни проблемни ситуации. Ефективно използват знанията си в сравнително нестандартен контекст. Свързват информация от различни източници и свободно я използват, като я преобразуват от един вид в друг. Демонстрират математическо мислене. Успешно изразяват идеите си с формалния език на математиката и последователно и задълбочено прилагат стратегии и подходи за решаване на проблеми в непознати ситуации. Детайлно описват, аргументират, представят и оценяват действията и изводите си. Могат да обяснят как и до каква степен полученото математическо решение е приложимо по отношение на реалната проблемна ситуация. |
| 5 | 607 | Учениците с резултати на пето равнище могат да разработват и използват математически модели в комплексни ситуации, като определят и разбират техните ограничения. Избират, сравняват и оценяват стратегии, подходящи за решаването на конкретни проблемни ситуации, свързани с тези модели. Учениците демонстрират добре развити умения за логическо мислене; задълбочено осмислят характеристиките на конкретната ситуация и планират действията си. Оценяват адекватно своята работа и ефективно формулират и представят решенията си и направените изводи. |
| 4 | 545 | Задачите на четвърто равнище изискват умения за работа с ясно формулирани математически модели, приложими при ясно дефинирани ситуации. Ситуациите могат да съдържат ограничения или да изискват правене на предположения. Учениците следва да избират и комбинират информация, представена по различни начини, включително и чрез символи, като я свързват със ситуации от реалния живот. Успешно формулират и представят обяснения и аргументи, които се основават на конкретни решения, интерпретации или действия. |
| 3 | 482 | За да решат задачите на трето равнище, учениците трябва да следват ясно описани процедури, включително и такива, които изискват вземане на конкретни решения. Като се основават на своите интерпретации, те изграждат прост модел или избират несложни стратегии за решаване на проблем. Учениците тълкуват и използват информация от различни източници, обясняват направените изводи. Показват умения за работа с проценти, дроби и пропорции. Представят по подходящ начин своите решения и произтичащите от тях изводи. |
| 2 | 420 | Учениците с резултати на това равнище тълкуват ситуации в контекст, който изисква да се направи пряк извод. Те извличат необходимата информация от конкретен източник и използват несложен модел за нейното представяне. Прилагат основни алгоритми, формули, процедури, за да решат задачи с цели числа. Справят се успешно със задачи, при които се изисква буквално тълкуване на получените резултати. |
| 1 | 358 | Учениците с резултати на първо равнище решават сравнително несложни математически задачи. Те отговарят на въпроси, формулирани в познат контекст, като необходимата информация е представена изчерпателно и ясно в условието на задачата. Могат да определят каква информация им е необходима за решаването на конкретна задача и да следват рутинни процедури при ясни и конкретни указания. Извършват действия, които произтичат непосредствено от условието на задачата. Задачите, които съответстват на първо равнище, са елементарни. Те обикновено изискват да се определи стойност по графика или в таблица, като критериите са пределно конкретни и връзката между графиката и описания в задачата контекст е ясно представена. След това те трябва да извършат несложни аритметични действия с цели числа, като следват инструкции. |
Дефиницията за природонаучната грамотност на PISA отразява разбирането за знанията и уменията, ценностите и нагласите, които се очаква младите хора да проявяват в ситуации, свързани с природните науки и технологиите за:
- Научно обясняване на природни процеси и явления;
- Планиране и оценяване на научно изследване;
- Научно тълкуване на данни и доказателства.
Емпиричното проучване е неделима част от науката и поради това е необходимо учениците да имат достатъчно познания за начините, по които се осъществява едно научно изследване, както и за процедурите, които се използват.
4 Tаблица 2. Скала за оценяване на постиженията на учениците по природни науки в PISA 2018:
| Равнище | Точки | Характеристика на равнището и задачите, оценяващи способностите на учениците |
| 6 | 708 | Учениците използват научни идеи и концепции от природните науки, за да обяснят или предложат хипотези за да обяснят непознати природни процеси или явления. Показват високо равнище на познавателни умения и научно мислене; използват знанията си за обосноваване на решения в непознат научен контекст. Когато тълкуват данни и факти, те разграничават приложима от неприложима информация и могат да използват знания извън учебните програми. Правят разлика между аргументи, основаващи се на научни факти и теории, и аргументи, основаващи се на други предположения. Преценяват правилно ли е замислен и планиран сложен експеримент, изследване или симулация на експеримент и аргументират оценката си. |
| 5 | 633 | Учениците използват абстрактни научни идеи или концепции, за да обяснят непознати и сравнително сложни явления и процеси, които включват няколко неочаквани връзки и зависимости. Прилагат теоретичните си знания, за да обяснят няколко възможности за извършване на експеримент, както и да аргументират избора на експеримент. Използват теоретично познание, за да тълкуват информация или да направят предположения. Преценяват кой е най-ефективният начин за научно изследване на проблем. Разбират ограниченията на научното изследване и тълкуването на данните. Тъй като разбират, че нито едно измерване не е напълно прецизно, могат да обяснят влиянието на грешката на измерването върху качеството на научните данни. |
| 4 | 559 | Учениците използват знания по природни науки (които може да са представени в условието на задачата), за да обяснят сравнително познати природни процеси и явления. Проблемът обикновено е ясно дефиниран. Могат да планират и осъществят експерименти, които включват използването на две или повече независими променливи. Могат да оценят доколко ефективно е планиран и проведен даден експеримент. Успешно тълкуват относително сложни и непознати бази данни; правят изводи, които произтичат от данните, и ги аргументират. |
| 3 | 484 | Учениците използват сравнително несложно познание, за да обяснят познати процеси и явления. При по-сложни или по-малко познати ситуации се справят с допълнителна помощ и подсказване. Използват отделни елементи на процедурно или теоретичното знание, за да проведат несложен експеримент. Разграничават въпроси, които могат да бъдат изследвани със средствата на науката, от въпросите, които не подлежат на научно проучване. |
| 2 | 410 | Учениците използват ежедневно познание и елементарни процедурни знания, за да направят изводи на базата на несложни експерименти и проучвания. Откриват връзката между несложен модел и явлението, което той представя. Тълкуват буквално резултатите от научно изследване или технологично решение. Използват познание, което им позволява да преценят дали даден проблем може да бъде изследван със средствата на науката. |
| 1А | 335 | Учениците имат ограничени знания и умения по природни науки, които използват в еднотипни и познати ситуации. С помощ могат да проведат предварително структуриран експеримент с не повече от две променливи. Идентифицират проста причинно-следствена връзка или корелация. Тълкуват графично представени данни, които изискват ниски равнища на когнитивните умения. Могат да определят кое е най-доброто научно обяснение на данни (от няколко предварително формулирани обяснения) в познат контекст. |
| 1В | 261 | Учениците използват елементарно и ежедневно познание по природни науки, за да разпознаят отделни аспекти на познати явления или процеси. Обикновено се затрудняват да определят основните характеристики на едно научно изследване. Използват само основни понятия по природни науки. Смесват личните си представи с научните факти, когато трябва да аргументират конкретен извод. Обясненията и заключенията, които правят, са очевидни и произтичат непосредствено от емпиричните данни. Могат да разпознаят елементарен модел от данни. Могат да осъществят несложен научен експеримент, като следват явни указания за действие. |