Кратки математически рутини за развиване на индуктивното мислене на учениците
Случвало ли ви се е да имате усещането, че учениците вземат решения “на автопилот”? Сякаш сте обяснили причинно-следствените връзки между променливите поне 100 пъти, но децата изобщо не разсъждават върху естеството на проблема, дават социално желателни отговори или просто стрелят в тъмното. Не се отчайвайте! Развиването на умения за даване на обосновани предположения и свързаното с тях индуктивно мислене е дълъг процес, който изисква усилия и постоянство, но също така може да бъде и забавен.
В тази статия ще ви предложим няколко кратки рутини за развиване на математическото мислене на учениците, които ще им помогнат за усъвършенстват своите индуктивни умения по един увлекателен и забавен начин.
Как индуктивното мислене помага за изграждането на обосновани предположения?
Изследването на математическите казуси включва откриването на зависимости, модели и структури. В началото могат да бъдат забелязани различни примери за функции, числа, форми или съотношения. С нарастването на техния брой, отделните парченца информация се наместват едно спрямо друго, за да образуват по-голяма, по-обща картина, в която всичко е свързано и съгласувано. На базата на направените наблюдения вече може да се състави хипотеза. По-нататъшното ѝ съпоставяне със сходни казуси позволява да се проследи тенденция и да се изгради научно-обосновано предположение. Иначе казано, формира се идея, която отразява множество наблюдения от сходни казуси. Именно този алгоритъм на разсъждения - от частното към общото, е известен като индуктивно мислене.
Как да развием индуктивното мислене на учениците?
Използването на математически рутини в часовете по математика помага за развиването на различните аспекти на математическото мислене, като същевременно създават позитивна среда за учене, комуникация и сътрудничество.
Ето няколко примера за математически рутини, с помощта на които можете да развиете индуктивното мислене на вашите ученици:
Вълшебни букви
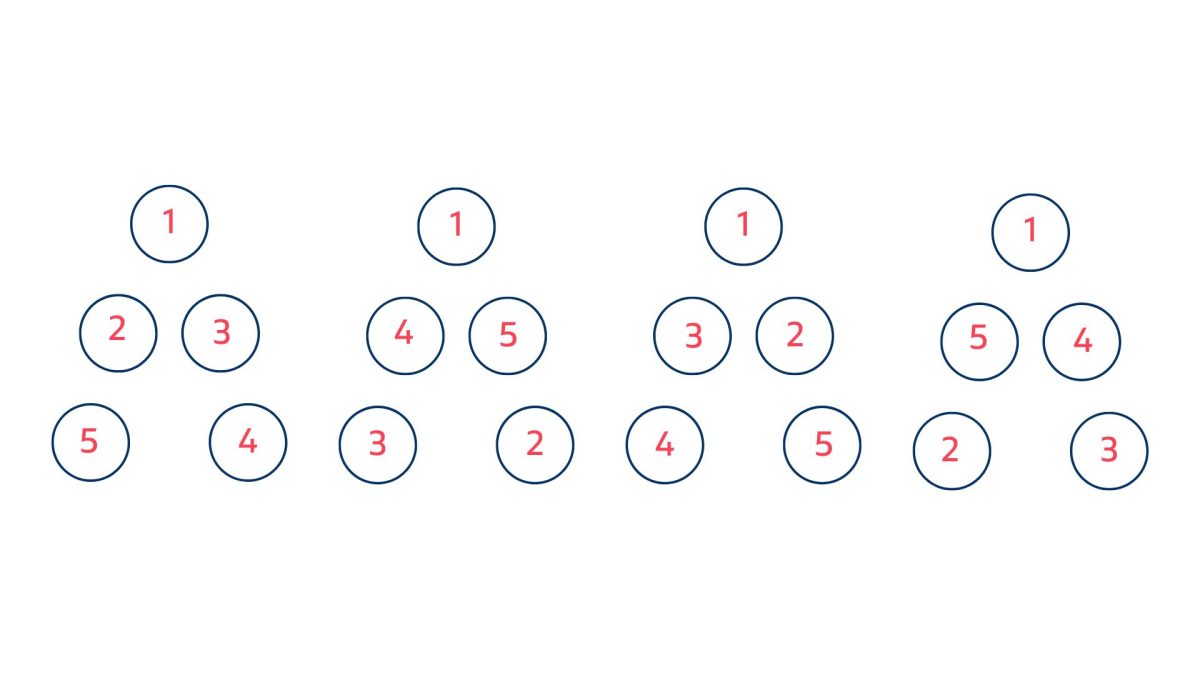
В тази математическа рутина учениците трябва да направят аргументирани предположения за алгоритъм на създаване на "вълшебни букви". Рутината напомня познатите магически квдрати, в които сборът от числата във всеки ред и колона е еднакъв. Учениците трябва да подредят числата от 1 до 5 по такъв начин, че да формират буквата Л и сборът на числата от двете рамена да бъде еднакъв.
- Насърчете учениците да открият възможно най-много варианти за решаване на казуса и запишете всяка правилна комбинация на дъската. Ето няколко примерни решения:
- Променете използваните числа. Изберете произволна последователност от 5 числа и изследвайте възможните комбинации (например 12-16, 36-40, 104-108).
- Могат ли учениците да открият някаква закономерност или тенденция при решаването на този тип задачи?
- Възложете на учениците да проверят дали изградената стратегия може да се приложи в при създаване на същата буква Л, но с по-голям брой последователни числа - 7, 9, 11 и т.н.
- Може ли по аналогичен начин да бъде изградена буквата Л, ако всяко от рамената съдържа 60, 1000 или повече последователни числа?
- На база проведените наблюдения и тестове учениците трябва да направят обосновано предположение за съставяне на буквата Л, независимо от броя на числата във всяко от рамената.
В следващ етап можете да предложите на учениците да направят аргументирани предположения за създаване на друга вълшебна буква, например Г, М или И.
Може ли да се достигне до някакво по-общо заключение, валидно за всички изследвани казуси?
Валсът на геометричните фигури
Нарисувайте на дъската квадрат с дължина на страната 10 cm. Оцветете този квадрат в цвят по избор и обяснете на учениците, че тази фигура няма да променя местоположението си по време на задачата. Нарисувайте втори квадрат със същите размери и го оцветете в различен цвят. Тази фигура ще танцува около първата, като винаги запазва контакт с нея и не променя пространствената си ориентация. Нарисувайте точка някъде върху обикалящия квадрат. В началото е по-добре да сложите точката върху някой от ъглите, защото така ще е по-лесно за учениците да си представят траекторията на движещата се фигура. Тяхната задача е да направят предположение за разстоянието, което точката ще измине, докато се върне в началното си местоположение.
- Разделете учениците в групи по двама и им дайте 1-2 минути, в които да си представят траекторията на точката. Посочете ученици, които да запишат на дъската идеите си.
- В рамките на 2-3 минути екипите трябва да тестват идеите си. За целта могат да нарисуват върху лист един квадрат и да изрежат още един, който да обикаля около първия. Можете също така да използвате интерактивен модел, показващ движението на втория квадрат и траекторията на точката.
- Може ли лесно да бъде пресметнат пътят на точката? Забелязва ли се някаква зависимост между формата, която се образува при движението на точката и изходните форми? Запишете хипотезите на дъската.
- Направените хипотези трябва да бъдат тествани, преди да се превърнат в обосновани предположения. За целта учениците трябва да проверят дали идеите им са приложими в сходни казуси. Ето няколко примера:
- променете размера на танцуващия квадрат. Какво се случва, ако той е по-голям от първия? Ами ако е по-малък?
- променете местоположението на точката. Същото разстояние ли ще измине, ако я поставите в друг ъгъл на квадрата или на произволно място върху някоя от страните му?
- променете вида на фигурите. Приложими ли са хипотезите, ако учениците използват два триъгълника или два шестоъгълника? Напомнете на екипите, че движещата се фигура няма право да променя пространствената си ориентация по време на преместването си.
- използвайте две различни по вид геометрични фигури, например квадрат и триъгълник, шестоъгълник и кръг и т.н. Приложими ли са хипотезите в този случай?
- Въз основата на проведените експерименти, учениците трябва да направят обосновани предположения за зависимостта между размерите на изходните форми и пътят, който изминава точката.
Шарени торбички
Тази рутина е свързана с намирането на закономерности при събирането на числа, които имат еднаква разлика помежду си. Учениците разполагат с четири торбички с различен цвят. Във всяка от тях има неограничен брой от дадено число. Например:
Учениците избират числа от различните торбички и ги събират. Не е необходимо да се вземат числа от всички торбички. Същевременно от всяка от тях може да се вземе неограничен брой числа.
- Посочете няколко ученици, които да запишат на дъската избраните от тях числа и полученият сбор. Има ли някаква закономерност в получените суми? Дискутирайте с класа и запишете няколко наблюдения на дъската.
- Разделете учениците в групи по двама. Всеки екип трябва да открие начин, по който:
- с помощта на четири от числата да получи сбор 16;
- да получи числото 25 при събирането на шест от числата;
- да определи коя от двете задачи е по-трудна и защо.
- Променете числата в торбичките на 1, 4, 7 и 10. Какви суми могат да се получат при сбора на три от числата? Някои вероятни отговори, които можете да получите са например 12, 21, 15, 18. Запишете на дъската наблюденията, които учениците могат да направят по отношение на получените числа.
- Направете същото упражнение, като увеличите броя на събираемите на четири, пет, шест и т.н.
- На базата на направените опити учениците трябва да помислят какви суми биха могли да се получат, ако броят на събираемите числа е 99 или 100.
- Ако числата в торбичките са 2, 5, 8 и 11, вместо 1, 4, 7 и 10, отговорът ще бъде ли различен?
- Въз основа на направеното изследване, учениците трябва да направят хипотези за това какви суми могат да се получат от сбора на числа с еднаква разлика помежду им. Запишете хипотезите да дъската.
- Предложете на учениците следните комбинации от торбички, с които да тестват генерираните идеи:
- Какви обосновани предположения могат да бъдат направени?
- Използвайки направените изводи, могат ли учениците да намерят бърз начин да проверят дали с числата 3, 7, 11 и 15 може да се получи сборът 412, ако се използват 30 събираеми?
Използването на математически рутини за развиване на индуктивното мислене на учениците дава възможност за проучване, анализиране, прогнозиране и доказване на определени зависимости между променливите. По този начин се подобрява разбирането и осмислянето на учебния материал, както и по-нататъшното му прилагане в нови за учениците казуси.
Допълнителен бонус е безопасната среда на сътрудничество, в която всички предложения са полезни за изграждане на хипотеза и обосновано предположение.
Непременно опитайте и вие!
За статията са използвани следните ресурси, които са допълнени с личния опит на автора: